情報処理技術者への道
これからIT関連の仕事を目指したいという人のために、折に触れ書いていきたいと思います(非定期更新ですのであんまり期待しないでください)
まずは2進数に慣れよう!
コンピュータの中身はすべて2進数で扱われますので2進数はとても重要な概念です。1桁の2進数はゼロかイチのどっちかを表す情報量の最小単位でありこれを「1ビット」と呼びます。
1桁の2進数:「1ビット」(0, 1の2通り)
2桁の2進数:「2ビット」(00, 01, 10, 11の4通り)
3桁の2進数:「3ビット」(000, 001, 010, 011, 100, 101, 110, 111の8通り)
~
n桁の2進数:「nビット」(2のn乗通り)
学校で習っているとおもいますけど、どんな10進数でも2進数で表せます。2で割って余りを並べていけばいいだけです。
例えば10進数の「5」は、2進数では「101」になります。でもコンピュータって電卓みたいに数字の計算をするだけじゃないですよね。数字以外に文字だって表現できるじゃないですか。で、例えばアルファベットの「A」は2進数で「1000001」に対応させると決めたのです。「B」は「1000010」に、そして「Z」は「1011010」に。これをアスキーコードといいます。つまりコンピュータとはゼロ・イチの並び方に特定の意味を持たせて利用する仕組みのことです。
16進数にも慣れよう
2進数を表現するには何しろ桁数が多くて表すのに大変です、紙面もいっぱいつかわにゃならんし、、、で16進数表記というものが考えられました。もちろんどんな2進数であっても10進数に1対1対応するので10進数で表記できるのですが、16進数表記には10進数表記にはない便利さがあるのです。16進数による表記は「4桁の2進数を1つの塊」として考える手法です。これであたかも10進数のような手軽さ(?)で2進数を表現できるようになるのです!
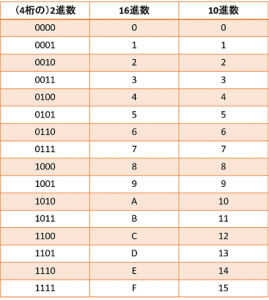
16進数の場合、10進数の10から15までの数はアルファベットのA~Fで表しますので下記のような表になります。(※このA~Fはアスキーコードとは関係ない)
アスキーコードの「A」は、7桁の2進数で「1000001」に対応させるという決めごとがありました。これを下のように連想してゆくと
「1000001」→「01000001」→「0100」「0001」となり、
これを16進数に当てはめると、「41」になります。
同様にアスキーコードの「Z」は「1011010」なので、
「0101」「1010」と解釈して、16進数では「5A」になります。
ここで16進数の「5A」ならまだしも、16進数の「41」といった場合、単に「41」と表記してしまうと10進数と区別がつかなくなって混乱してしまいます。そこで16進数の場合は、先頭に0xをつけて「0x41」とか、もしくはお尻にHをつけて「41H」とかで16進数であることを明示します。(アセンブラではHを、それ以外のプログラミング言語では0xを付けることが一般的なようです)
大昔のCPUはアドレスバスが16本しかなかったので、2進数で16桁分のアドレス空間しかありませんでした。2進数16桁ということは、取りうるアドレスが
「0000 0000 0000 0000」~「1111 1111 1111 1111」
16進数だと「0x0000」 ~「0xFFFF」
10進数だと「0」~「65535」
つまり64kバイトのアドレス空間しかなかったのです!
その後時代は降ってCPUのアドレス空間は32ビットに広がって
「0000 0000 0000 0000 00000 00000 0000 0000」~
「1111 1111 1111 1111 1111 1111 1111 1111」
16進数だと「0x00000000」~「0xFFFFFFFF」
10進数だと「0」~「4294967295」
4.3Gバイトのアドレス空間が得られるようになったのです。
(もちろん今では4.3Gバイトを超えるアドレス空間を持つCPUが普通です)
情報処理技術者を目指そうとするなら、まずは2進数・16進数について十分な理解をしておくことが重要です。
論理演算
2進数とは0と1の羅列でコンピュータの超々基本であることは述べましたけど、では0と1を使ったお遊びを考えます。まず入力信号Aと入力信号Bの2つがあって、その2つの入力値を元に出力される信号Cがあったとします。
ここで、AとBが両方とも1の場合はCに1が出力され、それ以外の場合はCに0が出力される場合を考えてみます。つまり、
A B → C
0 0 → 0
0 1 → 0
1 0 → 0
1 1 → 1
このような機能(ファンクション)を論理積(AND)と呼びます。
また、少なくともABどちらか一方だけが1であればCは必ず1で、AB両方とも0の時だけCが0になる場合、つまり
A B → C
0 0 → 0
0 1 → 1
1 0 → 1
1 1 → 1
を論理和(OR)と呼びます。
ついでに、
A B → C
0 0 → 0
0 1 → 1
1 0 → 1
1 1 → 0
を排他的論理和(XOR)と呼びます。排他的論理和(XOR)は2つの入力値が一致した時は0、一致しない時は1が出力されると覚えればOKです。
さらに論理積(AND)を完全に反転した機能、つまり
A B → C
0 0 → 1
0 1 → 1
1 0 → 1
1 1 → 0
を論理積の否定(NAND)と呼びます(NOT ANDの意味)
